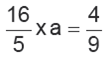6. Sınıf Matematik 1. Tema Çalışmaları

Matematik 1. Tema
Doğal Sayıların Çarpanları ve Katları Testi
Doğal Sayıların Çarpanları ve Katları Testi
Bir Doğal Sayının Çarpanları ve Katları Testi
Ortak Bölenler ve Ortak Katlar Testi
Asal Sayılar ve Asal Çarpanlar Testi
Asal Sayılar ve Asal Çarpanlar Testi
Kesirlerle Toplama İşlemi Kazanım Testi
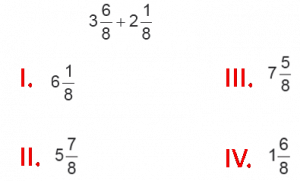
Kesirlerle Çıkarma İşlemi Kazanım Testi
Kesirlerle Çarpma İşlemi Kazanım Testi
Kesirlerle Bölme İşlemi Kazanım Testi
Kesirlerde Sıralama Kazanım Testi
Kesirlerin Ondalık Gösterimi Kazanım Testi
Ondalık Gösterimleri Çözümleme Kazanım Testi
Ondalık Gösterimleri 10, 100 ve 1000 ile Kısa Yoldan Çarpma ve Bölme İşlemi Kazanım Testi
Ondalık Gösterimleri Verilen Sayılarla Çarpma İşlemi Kazanım Testi
Ondalık Gösterimleri Verilen Sayılarla Bölme İşlemi Kazanım Testi
Bir Doğal Sayının Çarpanları ve Katları
Bir doğal sayının çarpanlarını ve katlarını belirlemek, matematiksel anlayışın temel taşlarından biridir. Bu konuda, bir sayının çarpanları ve katları arasındaki farkı anlamak kritiktir. Çarpanlar, bir sayıyı bölen doğal sayılardır. Örneğin, 12 sayısının çarpanları 1, 2, 3, 4, 6 ve 12’dir. Bu sayılar, 12’yi böldüklerinde kalan sıfır olur. Katlar ise bir sayının kendisiyle çarpılarak elde edilen sayılardır. Örneğin, 5 sayısının katları 5, 10, 15, 20 şeklinde devam eder.
Çarpanları ve katları belirlemek, matematiksel problemlerin çözümünde sıklıkla kullanılan bir beceridir. Çarpanları bulmak için sayının asal çarpanlarına ayrılması gerekmektedir. Örneğin, 30 sayısını ele alalım. 30’un asal çarpanları 2, 3 ve 5’tir, dolayısıyla 30 = 2 x 3 x 5 şeklinde yazılabilir. Bu aynı zamanda sayıların bölünebilme kurallarını öğrenmek ve uygulamak için de önemlidir.
Öğrenciler, çarpanlar ve katlar konusunu anlamak için çeşitli yöntemler kullanabilirler. Örneğin, çarpan ağaçları oluşturmak, çarpanları bulmada etkili bir yöntemdir. Aynı şekilde, sayı doğrusu üzerinde katları işaretlemek, bu kavramı görsel olarak anlamalarına yardımcı olabilir. Pratik yapmanın önemi bu konuda büyüktür. Öğrenciler, çeşitli sayıların çarpanlarını ve katlarını belirleyerek bu beceriyi geliştirebilirler.
Örnek bir problem üzerinden bu konuyu pekiştirelim: 24 sayısının çarpanlarını belirleyelim. 24’ün çarpanları 1, 2, 3, 4, 6, 8, 12 ve 24 olarak sıralanabilir. Aynı şekilde, 24’ün katlarını belirlemek istersek, 24, 48, 72, 96 şeklinde devam eden bir dizi elde ederiz. Bu tür örnek problemler ve çözümler, konunun daha iyi anlaşılmasını sağlar.
Bölünebilme Kuralları
Bölünebilme kuralları, bir sayının belirli bir sayıya tam olarak bölünüp bölünemeyeceğini hızlı bir şekilde belirlememize yardımcı olan matematiksel kriterlerdir. Bu kurallar sayesinde, uzun bölme işlemleri yapmadan bir sayının 2, 3, 4, 5, 6, 9 ve 10 gibi sayılara bölünebilir olup olmadığını kolayca anlayabiliriz. İşte bu yaygın bölünebilme kurallarının detaylı açıklamaları ve örnekler:
2 ile Bölünebilme: Bir sayı, son rakamı çift (0, 2, 4, 6, 8) ise 2 ile bölünebilir. Örneğin, 128 sayısı son rakamı 8 olduğu için 2 ile bölünebilir.
3 ile Bölünebilme: Bir sayının rakamları toplamı 3’ün katı ise, o sayı 3 ile bölünebilir. Örneğin, 123 sayısının rakamları toplamı (1+2+3=6) 3’ün katı olduğundan 3 ile bölünebilir.
4 ile Bölünebilme: Bir sayının son iki rakamı 4’ün katı ise, o sayı 4 ile bölünebilir. Örneğin, 312 sayısının son iki rakamı 12 olduğu için 4 ile bölünebilir.
5 ile Bölünebilme: Bir sayının son rakamı 0 veya 5 ise, o sayı 5 ile bölünebilir. Örneğin, 225 sayısının son rakamı 5 olduğu için 5 ile bölünebilir.
6 ile Bölünebilme: Bir sayı hem 2 hem de 3 ile bölünebiliyorsa, o sayı 6 ile de bölünebilir. Örneğin, 54 sayısı hem 2 hem de 3 ile bölünebildiği için 6 ile de bölünebilir.
9 ile Bölünebilme: Bir sayının rakamları toplamı 9’un katı ise, o sayı 9 ile bölünebilir. Örneğin, 729 sayısının rakamları toplamı (7+2+9=18) 9’un katı olduğundan 9 ile bölünebilir.
10 ile Bölünebilme: Bir sayının son rakamı 0 ise, o sayı 10 ile bölünebilir. Örneğin, 140 sayısının son rakamı 0 olduğu için 10 ile bölünebilir.
Bu bölünebilme kuralları, matematiksel işlemleri kolaylaştırmanın yanı sıra, günlük hayatta da çeşitli alanlarda kullanılabilir. Örneğin, büyük miktarların daha küçük gruplara ayrılması gereken durumlarda veya sayısal verilerin analizinde bu kurallar oldukça işlevseldir. Öğrenciler için ise, bu kuralları öğrenmek ve uygulamak matematiksel düşünme becerilerini geliştirme açısından son derece önemlidir.
Asal Sayılar ve Asal Çarpanlar
Asal sayılar ve asal çarpanlar, matematiğin temel taşlarından biridir ve sayılar teorisinin önemli bir parçasını oluşturur. Asal sayılar, sadece 1 ve kendisi dışında başka hiçbir pozitif tam böleni olmayan sayılardır. En küçük asal sayı 2 olup, ardından 3, 5, 7 gibi diğer asal sayılar gelir. Bu sayılar, pozitif tam bölenleri sınırlı olduğu için, matematiksel analizlerde ve çeşitli algoritmalarda büyük önem taşır.
Asal çarpanlar ise bir sayının asal sayı çarpanlarına ayrılması işlemini ifade eder. Örneğin, 28 sayısını ele alalım. Bu sayı, asal çarpanlarına şu şekilde ayrılabilir: 28 = 2 x 2 x 7. Burada 2 ve 7 asal sayılardır ve 28’in asal çarpanları olarak adlandırılır. Bu yöntem, sayıların faktorizasyonu olarak bilinir ve birçok matematiksel problemde kullanılır.
Asal çarpanları belirlemek için kullanılan en yaygın yöntemlerden biri, asal çarpanlara ayırma yöntemidir. Bu yöntemde, bir sayı en küçük asal sayıdan başlayarak bölünür ve bu işlem, sayı tamamen asal çarpanlara ayrılana kadar devam eder. Örneğin, 60 sayısını ele alalım:
- 60, 2’ye bölünür: 60 ÷ 2 = 30
- 30, 2’ye bölünür: 30 ÷ 2 = 15
- 15, 3’e bölünür: 15 ÷ 3 = 5
- 5, asal bir sayı olduğu için bölme işlemi sona erer.
Bu durumda, 60 sayısının asal çarpanları 2, 2, 3 ve 5’dir.
Asal sayıların matematikteki önemi, sadece faktorizasyon işlemlerinde değil, aynı zamanda kriptografi, bilgisayar bilimi ve mühendislik gibi birçok alanda da kendini gösterir. Asal sayıların benzersiz özellikleri, veri güvenliği ve şifreleme algoritmalarında kritik bir rol oynar.
Öğrencilerin asal sayılar ve asal çarpanlar konusunu daha iyi anlamaları için çeşitli alıştırmalar ve testler oldukça faydalıdır. Bu alıştırmalar, konunun pekiştirilmesine ve daha kolay kavranmasına yardımcı olur. Örneğin, verilen bir sayının asal çarpanlarını belirleme veya asal sayılarla ilgili problemleri çözme gibi egzersizler, öğrencilerin bu konudaki yetkinliklerini artıracaktır.
Konu Testleri ve Çalışma Önerileri
6. sınıf matematik 1. ünite konularını içeren testler, öğrencilerin bilgi seviyelerini ölçmeleri ve eksiklerini tespit etmeleri açısından oldukça önemlidir. Her konu için hazırlanan testler, öğrencilerin konuyu ne kadar anladıklarını belirlemelerine ve eksik oldukları noktaları görmelerine yardımcı olur. Bu nedenle, düzenli aralıklarla test çözmek, öğrenilen bilgilerin pekiştirilmesi açısından faydalıdır. Öğrenciler, konuları çalıştıktan sonra test çözerek konuyu tekrar edebilirler ve yanlış yaptıkları sorular üzerinde durarak eksiklerini giderebilirler.
Etkili çalışma teknikleri, zaman yönetimi ve sınav stratejileri de başarılı olmanın anahtarlarıdır. Çalışma sürecinde belirli bir plan oluşturmak, hangi konuların öncelikli olduğunu belirlemek ve bu plana sadık kalmak, öğrenmeyi daha verimli hale getirir. Örneğin, her gün belirli bir saat aralığında matematik çalışmak ve bu süreyi verimli kullanmak, ders başarısını artıracaktır. Ayrıca, düzenli tekrarlar yapmak, bilgilerin uzun süreli hafızada kalmasını sağlar.
Zaman yönetimi, sınavlarda başarıyı etkileyen önemli faktörlerden biridir. Test çözerken süre tutmak ve belirli bir zaman diliminde soruları yanıtlamak, sınav stresini azaltır ve zaman baskısıyla başa çıkmayı öğretir. Bunun yanı sıra, zor sorularla vakit kaybetmemek ve öncelikle kolay soruları çözmek, sınav süresini daha etkili kullanmayı sağlar.
Sınav stratejileri arasında ise soruları dikkatli okuma, verilen bilgileri doğru yorumlama ve işlem hatalarından kaçınma gibi unsurlar yer alır. Ayrıca, sınav esnasında sakin kalmak ve panik yapmamak da önemlidir. Öğrenciler, sınav öncesinde deneme testleri çözerek bu stratejileri uygulayabilir ve sınav sırasında daha başarılı olabilirler.