4. Sınıf Kesirleri Karşılaştırma Çalışma Yaprağı PDF
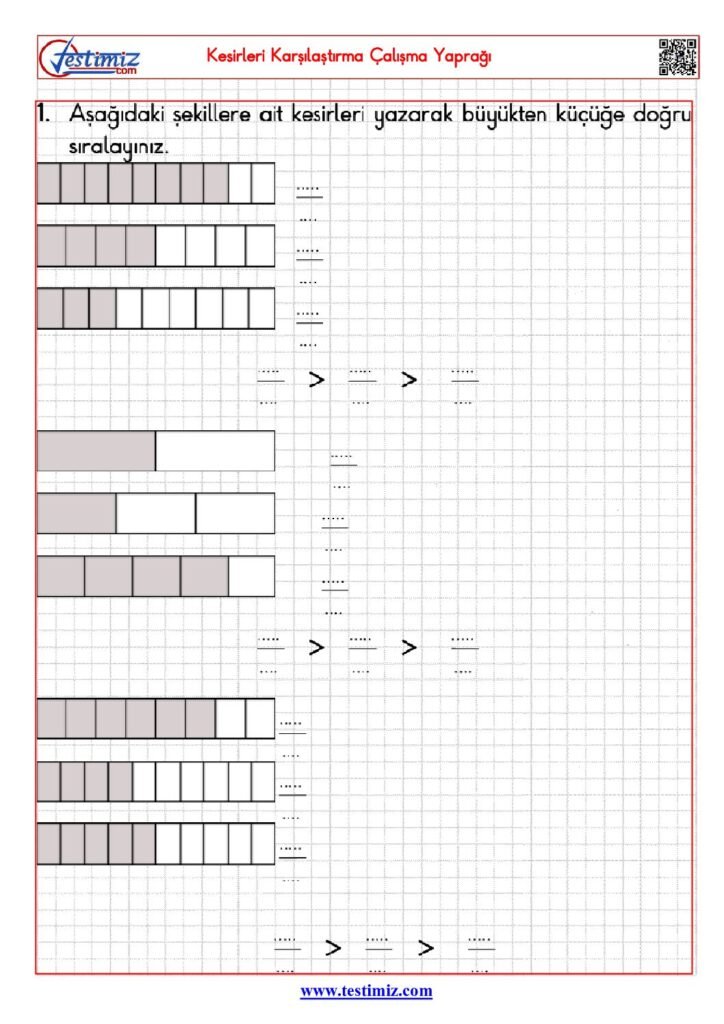
Kesirleri Karşılaştırma
Büyük Kesirler ve Tanımları
Büyük kesirler, matematikte kesir sayılarının birbirleriyle karşılaştırılmasında önemli bir yere sahiptir. Bir kesrin büyüklüğünü belirlemek için pay ve paydayı göz önünde bulundurmak gerekir. Genellikle bir kesir, hem payı hem de paydası arasındaki ilişkiye bağlı olarak büyük veya küçük olarak sınıflandırılır. Büyük bir kesir, aynı paydaya sahip olan diğer kesirlerin paylarıyla karşılaştırıldığında büyük paya sahip olan kesirdir.
Büyük kesirleri tespit etmek için en vizyolojik yöntemlerden biri kesirleri paydaları eşit olacak şekilde genişletmektir. Örneğin, 1/3 ve 2/5 kesirlerini karşılaştıralım. Öncelikle bu kesirlerin paydalarını eşitlemek gereklidir. Bu durumda, her iki kesrin paydasını 15 yapmak uygun olur. Yani, 1/3 kesri, 5/15 olarak genişlerken, 2/5 kesri 6/15 olarak genişler. Bu sayede 5/15 ve 6/15 kesirlerini kıyaslamak kolaylaşır ve 6/15 kesrinin daha büyük olduğu tespit edilir.
Büyük kesirlerin tespiti ve karşılaştırılması matematiksel düşünme becerisinin yanı sıra pratik ve sistematik yaklaşımlar kullanılarak da yapılabilir. Öğrenciler, şekil ve görseller kullanarak kesirleri karşılaştırabilirler. Bu görseller sayısal verilerin somut olarak görülmesini sağlar ve soyut matematiksel kavramların daha anlaşılır hale gelmesine yardımcı olur. Örneğin, pasta dilimleri veya grafiklerle kesirleri temsil etmek, öğrencilerin büyük kesirleri daha kolay belirlemelerini sağlar.
Kesirlerin karşılaştırılmasında dikkat edilmesi gereken önemli noktalar bulunur. Paydaları eşit olan kesirlerde, büyük kesri tespit etmek için paylara bakılır ve büyük paya sahip olan kesir daha büyük kabul edilir. Farklı paydalara sahip kesirlerde ise paydalar eşitlenerek karşılaştırma yapılır. Ayrıca fraksiyon çemberleri veya kesir çizgileri kullanarak görsel olarak da karşılaştırma yapılabilir. Bu yöntemler, öğrencilerin kesirleri büyükten küçüğe ya da küçükten büyüğe kolayca sıralamalarına yardımcı olur.
Küçük Kesirler ve Özellikleri
Küçük kesirler, matematiksel olarak bir bütünün daha küçük parçalarını temsil eder. Bu kesirler, payın paydadan küçük olduğu durumlarda ortaya çıkar. Örneğin, 1/4 ya da 2/5 gibi kesirler küçük kesirler kategorisinde değerlendirilir. Küçük kesirlerin belirlenmesi için kesrin payının, paydasının tam sayısından daha küçük olması gerekir. Bu tür kesirler genellikle bir olay ya da nesnenin bir kısmını ifade etmek için kullanılır.
Küçük kesirlerin tespitinde önemli metotlardan biri, pay ve payda arasındaki ilişkiyi gözlemlemektir. Bir kesir, küçük kesir olarak nitelendirilebilmesi için payı paydasından küçük olmalıdır. Örneğin, 3/7 kesiri, 3 sayısının 7 sayısından küçük olması nedeniyle küçük kesir olarak kabul edilir. Payın ve paydanın tümü tam sayılar olmalıdır ve herhangi bir basit kesir, küçük kesir olduğunda bu ilişki net bir şekilde gözlemlenebilir.
Küçük kesirlerin karşılaştırılmasında farklı metodlar kullanılabilir. En yaygın yöntemler arasında payları eşitleme yöntemi ile karşılaştırma ve paydaları eşitleme yöntemi yer alır. Payları eşitlemek için, birden fazla küçük kesirin ortak paydası bulunur ve paylar bu ortak paydaya göre ayarlanır. Karşılaştırma sonucunda, payı büyük olan kesir daha büyük kabul edilir. Aynı mantığın paydaları eşitleme yöntemi için de geçerli olduğunu söylemek mümkündür. Bu yöntemde, kesirlerin paydaları eşitlenene kadar genişletilir ve daha sonra paylara göre karşılaştırma yapılır. Payı küçük olan kesir küçük kabul edilir.
Öğrencilerin küçük kesirleri daha iyi anlamaları için çeşitli örneklerle çalışmaları faydalıdır. Örneğin, 1/4 ve 1/6 kesirlerini inceleyerek, 1/4’ün 1/6’dan büyük olduğunu görebilirler çünkü paydası daha küçük olan kesir daha büyük parçalara böler. Bu tür örnekler, küçük kesirlerin özelliklerini daha iyi kavramalarını sağlar ve karşılaştırma yöntemlerini pekiştirir.
Kesirleri küçükten büyüğe sıralama, matematik dünyasında öğrencilere sıklıkla karşılaştıkları ve anlamaları gereken önemli bir konudur. Bu konseptin özü, farklı büyüklükteki kesirlerin karşılaştırılması ve değerlendirilmesini içerir. Kesir sıralama stratejileri, öğrencilerin kolaylıkla farklı kesirler arasında karşılaştırma yapabilmelerini sağlar. İlk olarak, kesirlerin paydalarını eşitlemek, kesirler arasında doğru bir sıralama yapmanın en etkili yollarından biridir.
Örneğin, 1/3, 2/5 ve 3/4 kesirlerini ele aldığımızda, paydalarını eşitleyerek karşılaştırma yapmak daha kolay olacaktır. Bu durumda, tüm kesirlerin paydalarını ortak bir değere (örneğin, 60) eşitlersek, sırasıyla 20/60, 24/60 ve 45/60 elde ederiz. Bu değerleri incelediğimizde, kesirlerin küçükten büyüğe sırasıyla 1/3 (20/60), 2/5 (24/60) ve 3/4 (45/60) olduğunu görürüz.
Diğer bir yöntem ise, kesirleri ondalık sayılara çevirerek karşılaştırmaktır. Bu yöntem de oldukça kullanışlıdır ve özellikle paydaların eşitlenemediği durumlarda kolaylık sağlar. Yukarıdaki kesir örneğinden devam edecek olursak, 1/3, 2/5 ve 3/4 kesirlerini ondalık hale getirdiğimizde, bu değerler sırasıyla yaklaşık olarak 0.33, 0.40 ve 0.75 olur ki bu da sırayla küçükten büyüğe sıralanmıştır.
Bu stratejilerin yanı sıra, öğrencilerin hata yapmamaları için dikkat etmeleri gereken bazı püf noktalar vardır. Kesirlerin pay ve paydalarının doğru bir şekilde belirlenmesi ve hesaplamaların özenle yapılması bu püf noktaların başında gelir. Aynı zamanda, büyükten küçüğe sıralamayı da öğrenmek önemlidir, çünkü bu da kesirler arasındaki anlayışlarını derinleştirir.
Öğrenciler bu sıralama yöntemlerini uygulayarak pratik yapma fırsatı bulacakları çeşitli alıştırmalar ve etkinlikler de bulunmaktadır. Bu çalışmalar, öğrencilerin konuyu daha iyi kavramalarına ve kesirlerle ilgili problem çözme becerilerini geliştirmelerine yardımcı olacaktır. Böylece, kesir kavramı daha anlaşılır ve sınıfta ya da sınavlarda karşılarına çıkan soruları daha kolay çözebilirler.
Kesirleri büyükten küçüğe sıralamak, öğrencilerin matematik becerilerini geliştirirken aynı zamanda problem çözme yeteneklerini de artırır. Bu bölümde, kesirlerin büyükten küçüğe sıralanması için temel adımları ve stratejileri inceleyeceğiz.
Kesirleri Anlama
Kesirleri sıralamak için öncelikle kesirlerin ne anlama geldiğini ve nasıl karşılaştırılacağını anlamak önemlidir. Kesirlerin paydaları aynı ise, payı büyük olan kesir daha büyüktür. Örneğin, 3/4 ve 1/4 kesirlerinden 3/4 daha büyüktür. Eğer paydalar farklı ise, kesirleri sıralamak biraz daha karmaşık hale gelir.
Üst ve Alt Payda Yöntemi
Eğer paydalar farklı ise, kesirleri karşılaştırmak için paydaları eşitlememiz gerekir. Bunu yapmak için her iki kesirin de payda değerlerini ortak bir değerde buluştururuz. Örneğin, 2/3 ve 3/5 kesirlerini büyükten küçüğe sıralamak için her iki kesirin de paydasını aynı değerde buluşturmak gereklidir. Bu iki kesir için ortak payda 15 olarak bulunabilir. Şimdi kesirler 10/15 ve 9/15 şeklinde sıralanabilir ve 10/15 kesiri daha büyüktür.
Ondalık Değerlere Dönüştürme
Bir diğer etkili yöntem ise, kesirleri ondalık değerlere dönüştürmektir. Kesirler, bölme işlemi yapılarak ondalık sayılara dönüştürülebilir. Ondalık sayılar karşılaştırıldığında daha büyük olan değere sahip kesir daha büyük olacaktır. Örneğin, 1/2 ve 2/5 kesirlerini karşılaştırmak için bunları sırasıyla 0.5 ve 0.4 şeklinde ondalık değerlere çevirebiliriz. Bu durumda 1/2 kesiri daha büyüktür.
Uygulamalar ve Alıştırmalar
Öğrencilerin kesir sıralama konusunu pekiştirmeleri için çeşitli alıştırmalar ve etkinlikler yapmaları faydalı olacaktır. Farklı kesirleri sıralamak için çalışma yaprakları kullanmak, oyunlar ve interaktif etkinliklerle bu konuyu eğlenceli hale getirmek öğrenmeyi kolaylaştırabilir. Özellikle 4. sınıf seviyesindeki öğrenciler için hazırlanmış çalışma kağıtları, kesirlerin büyükten küçüğe sıralanmasını adım adım pratik etmelerini sağlar.