4. Sınıf Basit Kesirler Çalışma Kağıdı PDF

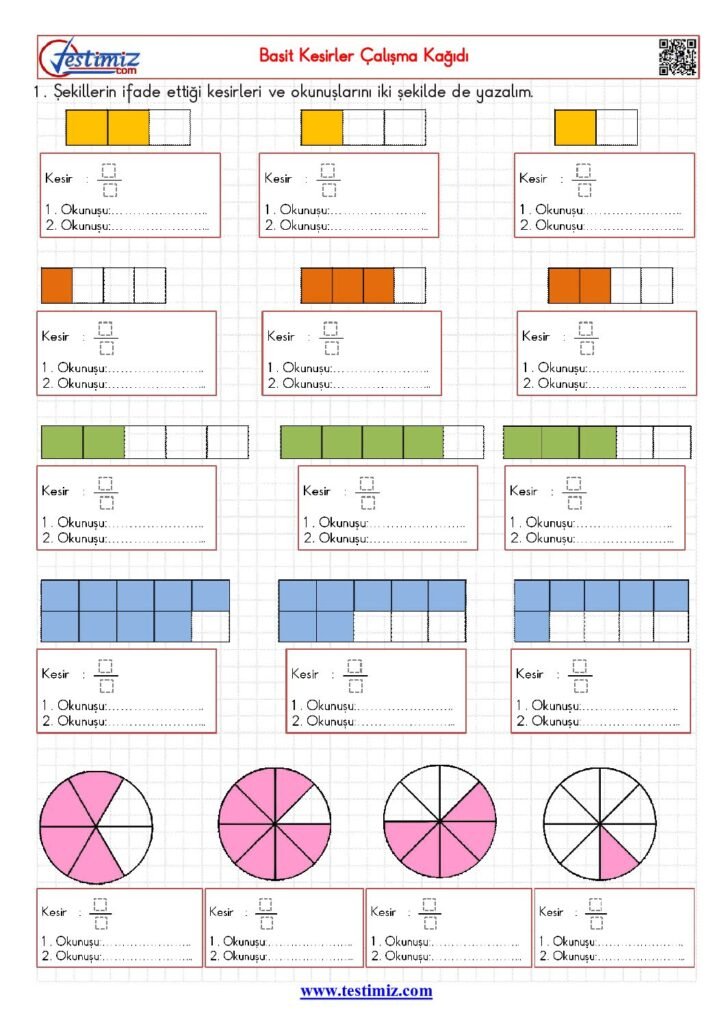
Basit Kesirler

İNDİR

Basit Kesirlerin Tanımı ve Örnekleri

Basit kesirler, payı paydasından küçük olan kesirlerdir. Matematiksel olarak ifade edildiğinde, bu tür kesirler bir tamsayının doğal olarak başka bir tamsayıya bölünmesi sonucu elde edilen bir orantı gösterir. Örneğin, 1/2, 3/4, ve 2/5 gibi kesirler basit kesirlerdir çünkü pay (üstteki sayı) her zaman paydadan (alttaki sayı) küçüktür.

Günlük yaşamda basit kesirler sıkça karşımıza çıkar. Bir pizza yediğinizi hayal edin; bu pizzayı dört eşit dilime böldüğümüzde bir dilimi ifade etmek için 1/4 kesirini kullanırız. Aynı şekilde, bir su bardağını ikiye böldüğümüzde ve sadece yarısını içtiğimizde, bu durumu 1/2 kesiri ile ifade ederiz. Bu örnekler, öğrencilerin basit kesirleri anlamalarına yardımcı olacak niteliktedir.

Basit kesirlerin temel özelliği, matematik terminolojisinde payın paydadan daima küçük olmasıdır. Diğer bir deyişle, basit kesirler daima birden küçüktür. Dolayısıyla, 5/6 veya 7/9 gibi kesirler de bu kategoriye girmektedir. Bu tür kesirleri şekillerle gösterdiğimizde, örneğin bir çemberi altı eşit parçaya böldüğümüzde ve sadece beş parçasını boyadığımızda, 5/6 kesirini görsel olarak ifade etmiş oluruz. Aynı mantıkla, 7/9 kesirini bir kareyi dokuz eşit parçaya bölüp yedisini boyayarak gösteririz.

Öğrencilerin basit kesirleri kavramaları, ileri düzey matematik konularında başarılı olmaları için temel bir adımdır. Bu nedenle, bu tür kesirlerin hem tanımsal hem de pratik örneklerle pekiştirilmesi önemlidir. 4. sınıf öğrencileri için özel olarak hazırlanmış çalışma kağıtları ve PDF dokümanları, bu konunun öğrenilmesini ve pekiştirilmesini daha etkili hale getirecektir.

Basit Kesirlerin Şekillerle Gösterimi

Basit kesirlerin şekillerle ifadesi, öğrencilerin anlamasını pekiştiren etkili bir yöntemdir. Bu bölümde, daire, kare ve dikdörtgen gibi geometrik şekiller kullanılarak kesirlerin nasıl gösterileceğini ele alacağız. Basit kesirler, payın paydadan küçük olduğu kesirlerdir. Bu tür kesirlerde, bir bütünün parçaları olarak ifade edilecektir.

Örneğin, 1/2 kesirini ele alalım. Bu, bir dairenin iki eşit parçaya bölünmesini ve bu parçalardan birinin boyanmasını gerektirir. Benzer şekilde, 1/4 kesiri bir karenin dört eşit parçaya bölünmesini ve bu parçalardan birinin gösterilmesini gerektirir. Öğrencilere bu kesirleri tanıtmak için, daire veya kare bölümlendirilerek gölgelenmiş alanların gösterilmesi çok önemlidir.

Dikdörtgenlerle de benzer bir yaklaşım uygulanabilir. Örneğin, 3/8 kesiri bir dikdörtgenin sekiz eşit parçaya bölünmesini ve bu parçalardan üçünün işaretlenmesini içerir. Geometrik şekiller yardımıyla bu tür örnekleri kullanarak, öğrenciler kesirlerin anlamını daha derinlemesine kavrayabilirler.

Öğrencilerin farklı şekillerde gösterim yapabilmeleri için çeşitli teknikler kullanılabilir. Örneğin, 2/3 kesirini temsil etmek için, iki parça gölgelenmiş üç eşit parçaya bölünmüş bir çember kullanılabilir. Bu kesir, farklı şekiller kullanılarak ifade edilebilir ve bunun üstünde çalışmak, öğrencilerin anlayışını genişletecektir.

Şekiller üzerinden anlatılan kesirlerin görselleri eklenerek anlamın güçlendirilmesi hedeflenmektedir. Her bir kesirin geometrik gösterimi öğrencilere hem görsel hem de kavramsal bir açıklık sağlayacaktır. Bu yöntem, basit kesirleri daha anlaşılır ve somut hale getirir, böylece öğrencilerin matematiksel kavramları uygulamalı olarak öğrenmeleri sağlanır.

Payı Paydasından Küçük Kesirlerin Karşılaştırılması

Basit kesirlerin karşılaştırılması, payı paydasından küçük olan kesirlerin büyüklüğünü belirlemede temel bir konudur. Bu kesirlerin büyüklüğünü karşılaştırmanın en etkili yolu, ortak bir paydaya getirilerek işlem yapmaktır. Örneğin, 1/4 ve 2/5 kesirlerini karşılaştırmak istiyorsak, her iki kesiri de ortak bir paydaya dönüştürmek gereklidir.

Ortak paydaya dönüştürme işlemine başlanmadan önce, kesirlerin paydalarını belirlemek gerekir. Örneğin, 4 ve 5 paydalarının ortak katı 20‘dir. Bu durumda, 1/4 kesiri 5/20 olarak, 2/5 kesiri ise 8/20 olarak dönüştürülür. Bu yeni kesirlerle karşılaştırma yapıldığında, 5/20‘nin, 8/20‘den küçük olduğu kolayca anlaşılır ve böylece 1/4 kesirinin 2/5 kesirinden küçük olduğu sonucuna varılır.

Bunun yanında, kesirlerin büyüklüklerini belirlerken payların eşitlenmesi de kullanılabilecek bir diğer yöntemdir. Örneğin, 3/7 ve 3/9 kesirlerini karşılaştırırken, payları aynı olduğu için paydası daha küçük olan kesirin daha büyük olduğu kolayca anlaşılır. Bu durumda, 3/7 kesiri, 3/9 kesirinden büyüktür.

Kesirlerin büyüklüklerini karşılaştırmada kullanılabilecek bir diğer pratik yöntem ise kesirleri ondalık sayıya dönüştürmektir. Örneğin, 2/3 ve 4/5 kesirlerini ondalık formata çevirirsek, 2/3 kesiri 0.666… ve 4/5 kesiri 0.8 olarak değerlendirilir. Bu durumda, 0.666…‘nın 0.8‘den küçük olduğu açıkça görülür ve böylece 2/3 kesiri 4/5 kesirinden küçüktür.

Çalışma kağıdında yer alacak örnek sorular ve problemler, bu yöntemlerin pratiğe dökülmesini sağlayacaktır. Öğrenciler, farklı kesir çiftlerini karşılaştırarak hangisinin daha büyük veya daha küçük olduğuna karar verecekleri alıştırmalar yapabilirler. Sorular, konu anlatımıyla desteklenirse öğrenmenin kalıcılığı artacaktır.

Çalışma Kağıdı: Alıştırmalar ve Cevap Anahtarı

4. sınıf basit kesirler konusunu pekiştirmek amacıyla hazırlanan çalışma kağıdı, öğrencilerin öğrendiklerini uygulamaları için geniş yelpazede alıştırmalar içermektedir. Bu çalışma kağıdı, farklı zorluk seviyelerine sahip kesir problemleri ve şekil üzerinde kesir gösterimleri sunarak, öğrencilerin temel kavramları anlamalarını sağlamaktadır.

Alıştırmalar bölümünde, başlangıç seviyesinden ileri seviyeye kadar değişen kesir problemleri bulunmaktadır. Basit kesirleri tanımlama ve karşılaştırma, kesirleri sayı doğrusunda gösterme gibi çeşitli konuları kapsayan sorular mevcuttur. Öğrenciler, şekiller üzerinden kesirleri belirleme ve kesirlerin pay ve paydalarını hesaplama gibi uygulamalar yaparak görsel ve matematiksel düşünme becerilerini geliştirebilirler.

Her sorunun hemen ardından ayrıntılı bir cevap anahtarı yer almaktadır. Bu cevap anahtarları, doğru çözüme ulaşılması için gerekli adımları içermekte ve öğrencilerin kendi çalışmalarını kontrol etmelerine olanak tanımaktadır. Bu sayede, öğrenciler yanlışlarını tespit edip düzeltmek için gerekli rehberliği alabilirler.

Çalışma kağıdının etkili kullanımı için öğretmen ve velilere yönelik bazı ipuçları ve öneriler de bulunmaktadır. Öncelikle, çalışma kağıdının çeşitli kesir problemleri ve şekil gösterimleri içermesi, öğrencilerin farklı öğrenme stillerine hitap etmektedir. Öğretmenler, ders sırasında bu çalışma kağıdını kullanarak öğrencilerin aktif katılımını sağlayabilir ve belirli konularda geri bildirim alabilirler. Veliler ise evde çocuklarıyla birlikte çalışarak, onların eksiklerini fark edip destek olma imkanı bulabilirler.

Bu kapsamlı çalışma kağıdı, 4. sınıf basit kesirler konusunu öğrenmek ve pekiştirmek için oldukça yararlı bir kaynaktır. Öğrenciler, bu alıştırmalar sayesinde hem eğlenceli hem de öğretici bir şekilde matematik becerilerini ileriye taşıyabileceklerdir.