4. Sınıf Toplama İşlemi Problemleri Testi
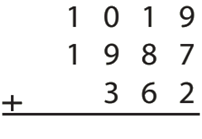
Toplama İşlemi
Temel Kavramlar: Toplama ve Çıkarma İşlemleri
Toplama ve çıkarma işlemleri, matematiğin en temel yapı taşlarından olup, aritmetik işlemler içinde önemli bir yer tutar. Toplama işlemi, bir dizi sayının toplamını veya bir araya getirilmesini ifade eder. Matematiksel olarak, iki veya daha fazla sayının toplamı alınarak, daha büyük bir sayıya ulaşılır. Örneğin, 2 + 3 = 5 işlemi, iki sayının birleşerek daha büyük bir sayı oluşturmasına örnektir. Toplama işlemi her zaman komütatif özellik gösterir, yani sayıların sırası değişse de sonuç aynı kalır (2 + 3 = 3 + 2).
Çıkarma işlemi ise, bir sayıdan diğerinin çıkarılması suretiyle fark bulunmasını ifade eder. Bir anlamda, çıkarma işlemi toplamanın tersidir. Örneğin, 5 – 3 = 2 işlemi, başlangıç sayısından belirli bir miktarın çıkartılmasıyla elde edilen sonucu gösterir. Çıkarma işleminin komütatif özelliği yoktur; yani, sayıların sırası değiştirilirse sonuç farklı olabilir (5 – 3 farklı, 3 – 5 farklıdır).
Toplama ve çıkarma işlemlerinde dikkat edilmesi gereken bazı önemli kurallar vardır. Öncelikle, işaretli (pozitif ve negatif) sayılar ile yapılacak işlemler sırasında dikkatli olunmalıdır. Pozitif ve negatif sayılar birlikte ele alınırken, işlemler dikkatle yapılmalı ve işaretlere dikkat edilmelidir. Örneğin, (-3) + 4 = 1 ve (-3) – 4 = -7 gibi işlemler, işaret kurallarına tabidir.
Bu işlemler sırasında, parantezlerin kullanımı da büyük önem taşır. Parantezler, işlemlerin öncelik sırasını belirler ve işlem hatalarının önüne geçilmesini sağlar. Örneğin, 3 + (4 – 2) işlemi, önce iç parantezdeki çıkarma işlemi yapılarak 3 + 2 sonucunu verir. Benzer şekilde, büyük sayı kümeleriyle çalışırken dikkat edilmesi gereken püf noktaları mevcuttur. Bu noktalar, toplama ve çıkarma işlemlerinde doğru sonuca ulaşmamızı sağlar.
Algoritmanın Yapısı: Toplama ve Çıkarma İşlemleri Adım Adım
Matematikte toplama ve çıkarma işlemleri, temel aritmetik becerilerini pekiştirmek için kritik öneme sahiptir. Bu bölümde, toplama ve çıkarma işlemlerinin algoritmalarını adım adım inceleyeceğiz. İlk olarak, toplama işleminin algoritmasına odaklanacağız.
Toplama İşlemi Algoritması
Toplama işlemi, matematiksel ifadelerin veya sayıların toplamını bulma sürecidir. Algoritmasını şu adımlar takip etmektedir:
- Sayıların Aynı Basamaklara Hizalanması: İşleme başlamadan önce, toplama yapılacak sayılar aynı basamaklar hizalanır. Örneğin, yüzler onlar ve birler basamağı düzgün bir şekilde alt alta getirilir.
- Sağdan Sola Doğru Toplama: İşleme en sağdaki basamaktan başlanır. Bu, birler basamağı ile başlar ve soldaki diğer basamaklara doğru ilerler.
- Elde Etme: Her basamakta toplanan sayıların sonucu 10’dan büyükse, bir sonraki basamağa bir eklenir. Bu işleme ‘elde etme’ denir ve sayının 10’dan büyük kısmı bir sonraki basamağa aktarılır.
- Sonuçlarının Yazılması: Her basamak için toplama işlemi tamamlandıktan sonra, sonuçlar alt alta yazılır ve toplam elde edilir.
Çıkarma İşlemi Algoritması
Çıkarma işlemi, bir sayıdan başka bir sayıyı çıkartarak farkı bulma sürecidir. Algoritmasını şu adımlar takip etmektedir:
- Sayıların Aynı Basamaklara Hizalanması: Çıkarma yapılacak sayılar aynı hizaya getirilir. Bu, işlemde hata yapılmasını önler.
- Sağdan Sola Doğru Çıkarma: İşlem sağdan sola, birler basamağından başlanarak yapılır.
- Borç Alma: Eğer çıkarılacak sayı daha büyükse, bir sonraki basamaktan borç alınır. Bu işlem ‘komşudan borç alma’ olarak adlandırılır ve çıkarılacak sayı ile borç alınan basamak ile işlem yapılır.
- Sonuçların Yazılması: Borç alma ve çıkarma işlemi tamamlandıktan sonra, sonucun her basamağı alt alta yazılarak fark bulunur.
Bu algoritmalar, toplama ve çıkarma işlemlerini sistematik ve düzenli bir şekilde yapmayı sağlar. Böylece, öğrenciler matematik problemlerini hata yapmadan çözebilirler.
Problemlerin Çözümü: Örnek Sorular ve Çözüm Yöntemleri
Toplama ve çıkarma işlemleri, 4. sınıf matematik derslerinde temel bir yer tutar. Bu kısımdaki örnek problemler ve çözüm yöntemleri, öğrencilerin bu konudaki anlayışlarını pekiştirmeyi hedefler.
Örnek Problem 1: Ahmet’in 23 tane kırmızı kalemi ve 17 tane mavi kalemi vardır. Toplamda kaç tane kalemi vardır?
Bu problemde, toplama işlemine ihtiyaç duyulmaktadır. Adım adım çözelim:
Adım 1: Verilen kalem sayısını yazın.
Kırmızı kalemler: 23
Mavi kalemler: 17
Adım 2: İki sayı toplanır.
23 + 17 = 40
Sonuç: Ahmet’in toplamda 40 kalemi vardır.
Örnek Problem 2: Ceyda’nın 85 tane topu vardı. Arkadaşı ona 12 tane daha top hediye etti. Ceyda’nın şimdi kaç topu var?
Bu problemde de toplama işlemine ihtiyaç duyulmaktadır. Adım adım çözelim:
Adım 1: Verilen sayıların not edilmesi:
Başlangıçtaki toplar: 85
Hediye edilen toplar: 12
Adım 2: İki sayı toplanır.
85 + 12 = 97
Sonuç: Ceyda’nın şimdi 97 topu var.
Örnek Problem 3: Bir çiftlikte 64 inek vardı. 24 inek satıldı. Şimdi çiftlikte kaç inek var?
Bu problemde çıkarma işlemi yapılmalıdır. Adım adım çözelim:
Adım 1: Verilen sayıların not edilmesi:
Başlangıçtaki inekler: 64
Satılan inekler: 24
Adım 2: İki sayı arasındaki fark bulunur.
64 – 24 = 40
Sonuç: Çiftlikte şimdi 40 inek var.
Öğrencilerin problem çözme becerilerini geliştirebilmeleri için aşağıdaki stratejilere dikkat etmeleri önerilir:
1. Problemi dikkatlice okuyup anlamak.
2. Bulunan bilgilerin not edilmesi ve daha sonra kullanılacak olan işlemlerin belirlenmesi.
3. Adımları takip ederek işlemleri yapmak ve sonucu kontrol etmek.
Bu yöntemler, öğrencilerin toplama ve çıkarma problemleri üzerinde etkili bir şekilde çalışabilmelerini sağlayacaktır.
İlişkilerin Kurulması: Toplama ve Çıkarma Algoritmalarının Bütünleştirilmesi
Toplama ve çıkarma işlemleri, matematiksel problemlerin temel taşlarıdır ve öğrencilerin bu işlemler arasındaki ilişkileri anlamaları, matematiksel becerilerinin gelişmesi için büyük önem taşır. Toplama ve çıkarma algoritmalarının bütünleştirilmesi, öğrencilerin bu iki işlem arasındaki mantıksal bağlantıları keşfetmelerine ve problemleri çözerken daha etkin bir şekilde kullanmalarına yardımcı olabilir.
Öğrencilerin kendi öz bilgileriyle toplama ve çıkarma işlemleri arasındaki ilişkiyi kurmalarını sağlamak, onların kavrayışlarını pekiştirecektir. Örneğin, bir toplama işleminin tersinin çıkarma işlemi olduğunu anlamak, öğrencilerin her iki işlemi de daha iyi kavramalarına yardımcı olur. “10’a 5 ekle” ve “15’ten 5 çıkar” işlemlerinin birbirinin tersi olduğunu fark etmek, öğrencilerin bu mantıksal bağlantıları daha çabuk kavramalarını sağlar ve problemleri çözerken bu bağlantılardan yararlanabilirler.
Toplama ve çıkarma işlemleri arasındaki benzerlikler ve farklar üzerinde durmak da önemlidir. Her iki işlem de sayıların büyüklüklerini değiştirmek amacıyla kullanılır, ancak toplama işlemi sayıları bir araya getirirken, çıkarma işlemi bir sayıyı diğerinden ayırma yoluyla farklı bir sonuç elde eder. Bu farklılıkların anlaşılması, öğrencilerin hangi işlemi ne zaman ve nasıl kullanacaklarını doğru bir şekilde belirlemelerine katkıda bulunur.
Sonuç olarak, toplama ve çıkarma algoritmalarını bütünleştirerek öğrencilerin bu işlemler arasındaki ilişkileri kurabilmeleri, matematiksel problemleri çözme becerilerini artırır. Öğrencilerin bu ilişkileri fark etmeleri ve uygulamaları, problem çözme süreçlerinde daha bilinçli ve etkili olmalarına yardımcı olur. Toplama ve çıkarma işlemlerinin mantıksal bağlantılarını anlamak, matematik eğitiminin temel hedeflerinden biridir ve bu bağlamda öğrencilerin algısal yeteneklerini geliştirmek, matematiksel başarılarını olumlu yönde etkiler.



Test çok güzel olmuş. Doğru cevapları hemen göstermesi iyi olmamış. Test bittikten sonra doğru cevapları göstermesi iyi olurdu.