4. Sınıf Üç Doğal Sayı ile Çarpma İşlemi Çalışması PDF

Üç Doğal Sayı ile Çarpma İşlemi

İNDİR

Çarpma İşleminin Temel Kuralları

Çocukların üç doğal sayıyı doğru ve etkili bir şekilde çarpabilmeleri için öncelikle çarpma işleminin temel kurallarını bilmeleri gerekmektedir. Çarpma işlemi, belirli matematiksel özelliklere sahip olup, bu özelliklerin iyi anlaşılması gereklidir. İşte bu temel kurallar ve özellikler:

Bir Sayının Kendisiyle Çarpılması: Herhangi bir doğal sayının kendisiyle çarpılması, sayının karesi olarak adlandırılır. Örneğin, 4 x 4 = 16. Bu temel kural, öğrencilerin çarpma işlemini daha hızlı ve pratik yapmalarına yardımcı olur.

Sıfır ile Çarpma Kuralı: Çarpma işleminde sıfır önemli bir rol oynar. Herhangi bir sayı sıfır ile çarpıldığında sonuç daima sıfırdır. Örneğin, 5 x 0 = 0 veya 0 x 7 = 0. Bu kuralın anlaşılması, öğrencilerin çarpma işlemi sorularını çözerken zaman kaybetmemelerini sağlar.

Bir ile Çarpma Kuralı: Bir sayının bir ile çarpılması durumunda sonuç yine o sayının kendisi olur. Bu kural, çarpma işleminin en basit halidir ve örnek olarak 7 x 1 = 7 veya 1 x 9 = 9 verilebilir. Öğrencilerin bu kuralı benimsemesi, büyük çarpma işlemlerinde bile hızlıca sonuca ulaşmalarını sağlar.

Örneklerle pekiştirilmesi, bu kuralların akılda kalıcılığını artırabilir. Örneğin, 3 x 4 x 1 işlemi, 12 x 1 = 12 olarak hesaplanır ve sonucu 12’dir. Başka bir örnek olarak, 6 x 0 x 5 işlemi, 0 ile çarpma kuralı nedeniyle sonuç sıfır olacaktır.

Bu kurallar, temel matematik becerilerinin geliştirilmesi için gereklidir ve öğrencilerin üç doğal sayıyla çarpma işlemini kolayca yapabilmelerini sağlar. Düzenli pratik yaparak ve çeşitli örnekler çözerek bu kuralların pekiştirilmesi sağlanmalıdır.

Üç Doğal Sayı ile Çarpma İşlemi ve Adımları

Üç doğal sayı ile çarpma işlemini doğru bir şekilde gerçekleştirebilmek için belirli adımları izlemek gerekmektedir. Öncelikle, üç sayının çarpılması süreci iki ana aşamadan oluşur. İlk olarak iki sayının çarpılması, ardından çıkan sonucun üçüncü sayı ile çarpılması şeklinde ilerler.

Örneğin, 2, 3 ve 4 sayılarıyla çarpma işlemi yapalım:

1. Adım: İlk iki sayıyı çarpın.
2 × 3 = 6

2. Adım: İlk adımda elde edilen sonucu üçüncü sayı ile çarpın.
6 × 4 = 24

Bu örnekten hareketle, üç doğal sayı ile çarpma işlemi şu şekilde özetlenebilir: İlk olarak iki sayıyı çarptıktan sonra bu sonucu üçüncü sayı ile çarpın. Bu adımları takip ederek, işlem yapılması gereken her durumda net bir sonuca ulaşılabilir.

Çocukların üç doğal sayı ile çarpma işlemini daha iyi anlamalarına yardımcı olmak için bazı ipuçları sunabiliriz. Öncelikle, karışıklığı önlemek adına işlemler sırasında parantez kullanımı oldukça faydalıdır. Parantezler, hangi işlemin önce yapılacağını belirleyerek hesaplamaların doğru bir sırayla yapılmasını sağlar.

Örneğin, (2 × 3) × 4 = 24 sonucunu elde etmek için ilk olarak parantez içindeki işlem yapılır, ardından çıkan sonuç üçüncü sayı ile çarpılır. Bu yöntem, özellikle birden fazla çarpma işleminin yer aldığı sorularda dikkat dağınıklığını önlemeye yardımcı olur.

Ayrıca, adımları tek tek uygulamak ve her adımın sonucunu kontrol etmek, hataların önüne geçmek adına oldukça önemlidir. Çocuklar bu yöntemi alışkanlık haline getirdiklerinde, üç doğal sayı ile çarpma işlemlerini daha hatasız ve güvenilir bir şekilde gerçekleştirebilirler.

Yan Yana Çarpma Tekniği

Üç doğal sayının yan yana çarpma tekniği, öğrencilere çarpma işlemlerini daha pratik ve hatasız bir şekilde gerçekleştirme imkanı sunar. Bu teknik, sayıların birbirine çarpılması ve sonuçlarının düzenli bir şekilde yazılması üzerine kuruludur. Örneğin, 2, 3 ve 4 sayılarının çarpımını ele alalım. Bu durumda, öncelikle ilk iki sayıyı çarparız: 2 x 3 = 6. Ardından, bu sonucu üçüncü sayıyla çarparız: 6 x 4 = 24. Böylece, 2 x 3 x 4 = 24 sonucuna ulaşmış oluruz.

Yan yana çarpma tekniğinin ayrıntılarına bakacak olursak, bazı temel kuralları ve prensipleri anlamak önemlidir. İlk olarak, çarpma işlemi yaparken sayıların büyüklüğü sırasıyla dikkate alınabilir. Küçük sayılarla başlayarak çarpma işlemlerini adım adım ilerletmek, işlemlerin daha kolay ve hızlı yapılmasını sağlar. Örneğin, 5, 2 ve 8 sayılarını çarparken, önce 5 x 2 = 10 işlemini yapabiliriz ve ardından bu sonucu 8 ile çarparız: 10 x 8 = 80. Bu yöntem, büyük sayılarla çarpmaktan kaçınarak işlemleri basitleştirir.

Bununla birlikte, bu teknikte yaygın olarak karşılaşılan bazı hatalar ve bu hataların düzeltilme yolları da vardır. En sık yapılan hata, sayıların çarpım sırasını yanlış belirlemektir. Öğrenciler genellikle büyük sayılarla çarpma işlemi yaparken zorlanır ve hatalar yapabilir. Bu durumu önlemek için, çarpılacak sayıları sıralayarak ve adım adım ilerleyerek dikkatli bir şekilde hesaplamalar yapmak gerekmektedir. Ayrıca, her adımda elde edilen sonuçları kontrol etmek, hataların derinleşmesini engeller ve doğru sonuca ulaşmayı sağlar.

Öğrencilerin yan yana çarpma tekniği ile ilgili pratik yapmaları, bu yöntemde ustalaşmalarını kolaylaştırır. Çeşitli örneklerle bol bol çalışma yapmak, çarpma işleminin mantığını daha iyi kavramalarına yardımcı olur ve alışkanlık kazandırır. Bu sayede hem çarpma işlemlerinde hızlarını artırabilir hem de doğru sonuçlar elde edebilirler.

Uygulama ve Pekiştirme: PDF Çalışmaları

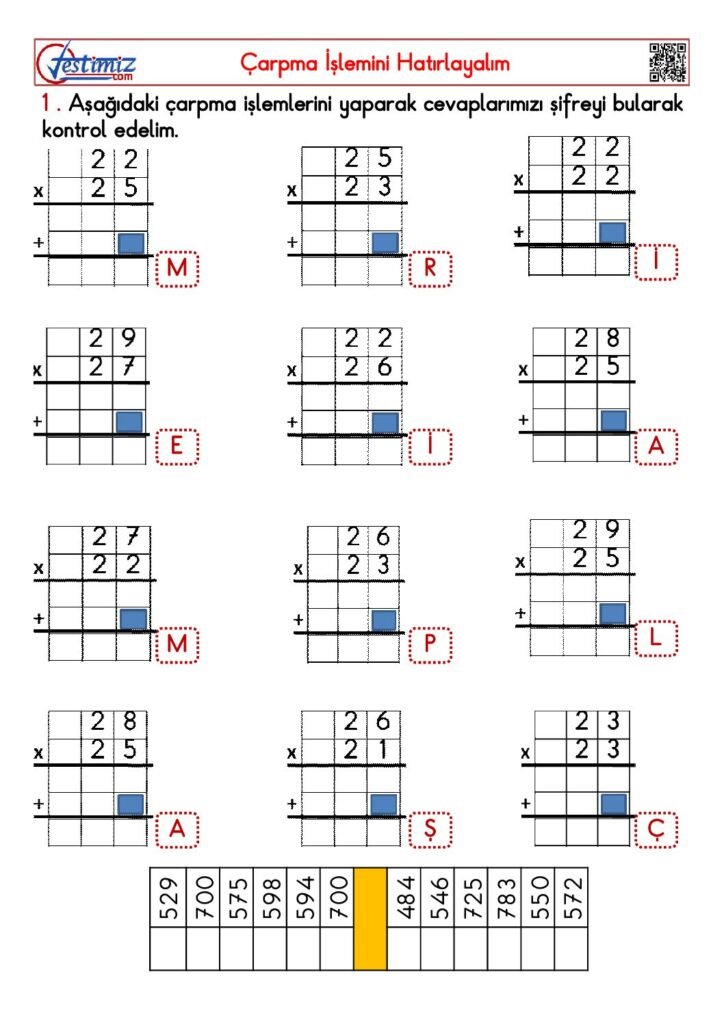
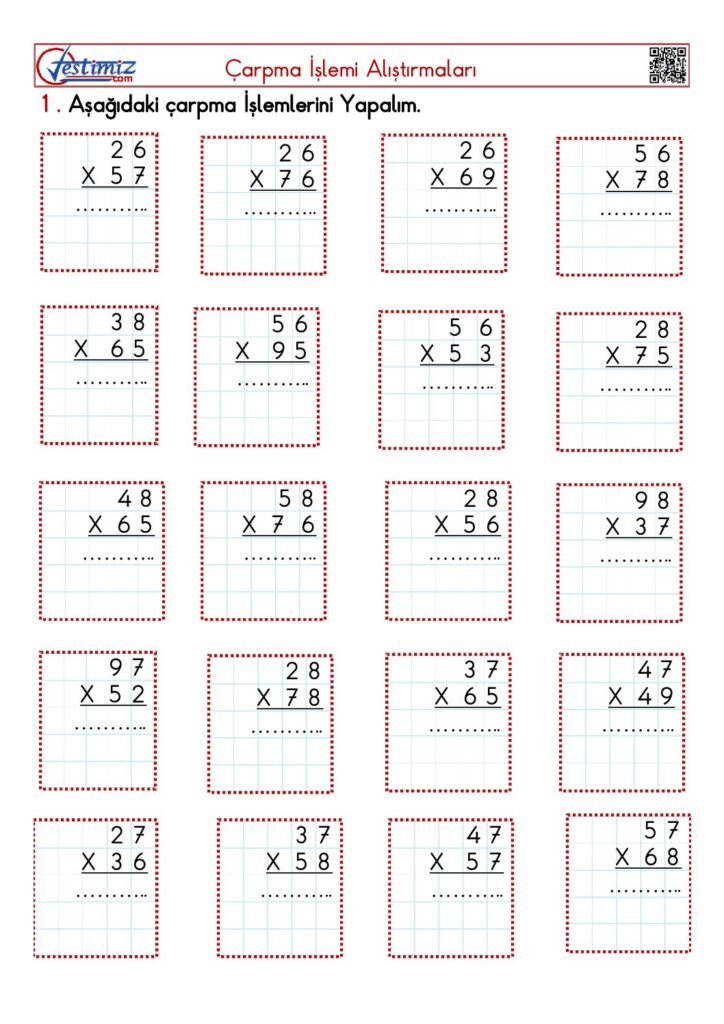
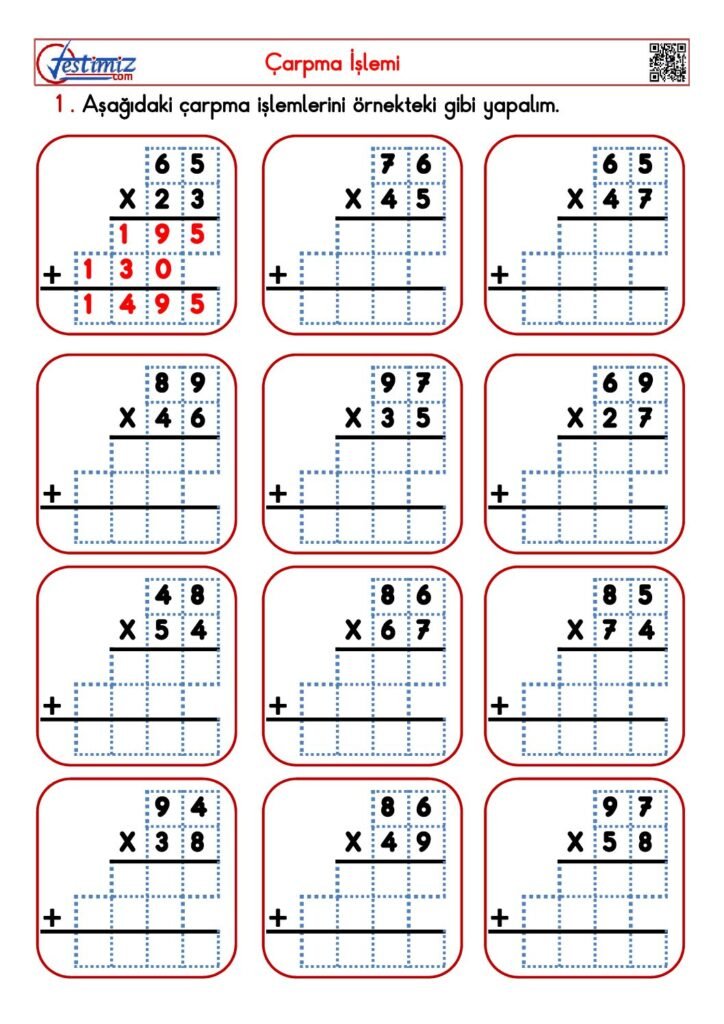
Matematik öğreniminde pekiştirme ve uygulama, öğrencilere kavramları daha iyi anlama ve zihinsel olarak içselleştirme fırsatı sunar. 4. sınıf düzeyinde üç doğal sayı ile çarpma işlemi üzerine odaklanan PDF çalışmaları, bu amaç doğrultusunda tasarlanmış etkin materyaller sunar. PDF dosyalarında, çeşitli çarpma alıştırmaları ve bu alıştırmaların çözüm anahtarları yer almaktadır. Bu çalışma dökümanları, öğrencilere teorik bilgi ile pratik uygulamayı harmanlayarak matematik başarısını artırmada önemli bir rol oynar.

PDF çalışmaları, öğrencilerin gün be gün düzenli olarak çalışabilecekleri şekilde tasarlanmıştır. Her çalışmada, farklı zorluk seviyesinde çarpma işlemleri bulunmaktadır ve bu sayede öğrenci, kendi hızında ilerleme kaydedebilir. Yan yana çarpma tekniği ile hazırlanan bu alıştırmalar sayesinde, hızlı ve doğru sonuçlar elde etme becerisi geliştirilir. Ayrıca, her PDF dosyasında bulunacak çözüm anahtarları, öğrencilerin kendi kendine kontrol edebileceği şekilde düzenlenmiştir. Bu sayede yanlışlarını görüp doğru yöntemi öğrenmeleri sağlanır.

Bu PDF çalışmalarını en verimli şekilde kullanabilmek için belirli bir günlük çalışma planına uymak önerilir. Örneğin, her gün belirli bir sayfa üzerinde çalışmak, düzenli tekrarlar ile hem bilgi kalıcılığını sağlar, hem de öğrencinin süreç içindeki gelişimini adım adım takip edebilmesini mümkün kılar. Ayrıca, öğrencilere belirli hedefler koymaları ve bu hedeflere ulaşma konusunda kararlı olmaları tavsiye edilir. Başarıya ulaşmada, sabır ve sürekliliğin önemini göreceklerdir.

Bunlara ek olarak, ailelerin de sürece dahil olmaları, çocukların motivasyonunu artırıcı bir etkendir. Çocuk ile birlikte çalışma sürelerini planlamak ve işbirliği yapmak, çarpma işlemleri üzerindeki pratiklerin daha keyifli ve öğretici olmasını sağlar. Bu kapsamlı ve düzenli matematik çalışmaları, öğrencilerin öğrenme yolculuğunda sağlam adımlarla ilerlemelerine destek olacaktır.